Figures, shapes and developments.
 In the figure shows how to build a tangential spheres in space. The centers of the spheres are the vertices of a regular polyhedron and their radii corresponding to half of each edge of the polyhedron.As the regular polyhedron has all have equal sides all have the same diameter spheres and simultaneously are tangent at the midpoint of each edge. The figure shows a regular icosahedron in plan, elevation and profile. At each vertex of the icosahedron is drawn as a sphere radius by taking half of the edge so that all areas are equal and tangent to each other.
In the figure shows how to build a tangential spheres in space. The centers of the spheres are the vertices of a regular polyhedron and their radii corresponding to half of each edge of the polyhedron.As the regular polyhedron has all have equal sides all have the same diameter spheres and simultaneously are tangent at the midpoint of each edge. The figure shows a regular icosahedron in plan, elevation and profile. At each vertex of the icosahedron is drawn as a sphere radius by taking half of the edge so that all areas are equal and tangent to each other.
If the polyhedron is Archimedean and therefore consists of regular polygons but also various regular (equal sides), the spheres have also the same size but remain tangent to one another, maintaining a greater distance between them being a major faces others like shown in this icosidodecahedron given in plan and elevation.
To draw tangents exercises spheres whose centers are on the same plane simply an exercise of tangent circles in the plane and give volume to them. http://tangencias-inversion . blogspot.com /
http://tangencias-potencia.blogspot.com/
http://tangencias-y-enlaces.blogspot.com/
http://teoremas-de-geometria.blogspot.com/2012/03/teoremas-de-arbelos.html
 The theorem of the leg on the ground is represented graphically, and goes on to say that the yellow rectangle and the blue square are equivalent means they have the same area ( http://figuras-equivalentes.blogspot.com/.)
The theorem of the leg on the ground is represented graphically, and goes on to say that the yellow rectangle and the blue square are equivalent means they have the same area ( http://figuras-equivalentes.blogspot.com/.)
represent the theorem of the leg in plan and in elevation give the same height at the two prisms. Have the same area as the base, having the same height are the same volume, so we calculated a cube that has the same volume as a prism. We take the equivalence theorem to calculate an equivalent and corresponding to its three-dimensional figures, this is by volume.
 The theorem of the leg on the ground is represented graphically, and goes on to say that the yellow rectangle and the blue square are equivalent means they have the same area ( http://figuras-equivalentes.blogspot.com/.)
The theorem of the leg on the ground is represented graphically, and goes on to say that the yellow rectangle and the blue square are equivalent means they have the same area ( http://figuras-equivalentes.blogspot.com/.)represent the theorem of the leg in plan and in elevation give the same height at the two prisms. Have the same area as the base, having the same height are the same volume, so we calculated a cube that has the same volume as a prism. We take the equivalence theorem to calculate an equivalent and corresponding to its three-dimensional figures, this is by volume.


As was done with the equivalent figures, we can follow the same procedure for proportional figures in space-that is, they have the same shape but different size (http://proporcion-escala-semejanza-homotecia.blogspot.com /).
built two homothetic figures (homologous improper axis), which means that they are proportionate and while its vertices are aligned with a projection center O. The construction of the homothetic figures do at the plant and the draw elevation corresponding vertical projections so that the two heights of the prisms are also aligned with the projection center O. As all segments or edges of the prisms are aligned at their vertices with the projection center O, this means that the figures are the same way but of different sizes, ie homothetic in space. dihedral system is the most adequate representation systems to draw the dimensions (measures) of the pieces, as it shows faces in true form (with actual dimensions or scale) that are not distorted by the effect of perspective. There are basic rules that we follow in order to understand the drawings: http://acotacion-normalizada.blogspot.com/
 .
.http://secciones-cortes-roturas.blogspot.com/

 The calculation of shadows and reflections in the dihedral system greatly facilitates the understanding of the drawings:
The calculation of shadows and reflections in the dihedral system greatly facilitates the understanding of the drawings:

 The calculation of shadows and reflections in the dihedral system greatly facilitates the understanding of the drawings:
The calculation of shadows and reflections in the dihedral system greatly facilitates the understanding of the drawings:http://calculo-de-reflejos.blogspot.com/
http://sombras-en-perspectiva-conica.blogspot.com/
 Part represented in plan, elevation and profile with auxiliary view and axonometric isometric perspective representation.
Part represented in plan, elevation and profile with auxiliary view and axonometric isometric perspective representation.
in axonometric drawing modes: http://perspectiva-axonometrica.blogspot.com/
http://perspectiva-caballera.blogspot.com/
http://sombras-en-perspectiva-conica.blogspot.com/
 Part represented in plan, elevation and profile with auxiliary view and axonometric isometric perspective representation.
Part represented in plan, elevation and profile with auxiliary view and axonometric isometric perspective representation.in axonometric drawing modes: http://perspectiva-axonometrica.blogspot.com/
http://perspectiva-caballera.blogspot.com/
 Here we see the shadow cast on the ground that produces a red rectangle to and an object consisting of two prisms parallelepipeds with their shadows thrown own, both objects are illuminated by the sun, which is in the direction making an angle d and h altitude above named the horizontal plane, its direction determined by its orthogonal projection d and d1 on the horizontal plane.
Here we see the shadow cast on the ground that produces a red rectangle to and an object consisting of two prisms parallelepipeds with their shadows thrown own, both objects are illuminated by the sun, which is in the direction making an angle d and h altitude above named the horizontal plane, its direction determined by its orthogonal projection d and d1 on the horizontal plane.Another parameter that determines the location of the sun is the angle g which forms the north-south line from the vertical plane containing the solar ray d, a this angle is called azimuth and counted in the direction of clockwise.
As shown in the drawing, the orthogonal projection of a sunbeam d1 on the horizontal plane of the ground, is the direction in which the shadows of the lines vertical prisms, in the drawing indicated with the letter m. While the direction of any solar ray d is projected onto the elevation in the direction n which is the direction of the shadow cast of a segment perpendicular to the vertical plane. In the picture we see in the dihedral system elements of the previous scene. As shown in the drawing, the sun is so distant that the rays are considered parallel, so the prism parallel lines create shadows, the shadows of the vertical lines are all parallel to the direction of the shadow cast as. The beam Sun is defined as any line in dihedral system, for his leadership in plant d1, d2 and direction in the elevation.The double prism and cast their own shadows and the quadrilateral parallelogram with red as its shadow on the horizontal plane. The north-south NS determined by the shadow cast as the ring, called azimuth angle g, which has from the north-south line to the right or clockwise to clockwise. The altitude h is in blue, and is the angle between the orthogonal projection of the solar ray on the ground, that is, the shadow as the horizontal plane, and the solar ray d1. As the plane containing these two lines is vertical swing it need to have their true magnitude. When you swing it get (d1), the angle between this line and d1 is the altitude of the sun and appears in true form after abatement plan. In this way the plant we determined the exact position of the sun, the angle g which is its direction from the north-south line in green (azimuth), and the angle h defines its direction relative to the horizontal plane and in blue (high).

 We observed a sundial and its construction. Gnomom a rod called shadow projected onto a plane or plane of the quadrant yellow, in this case horizontal. S called a blue plane is perpendicular to the rod and describes the sun's path in a complete circle, this means covering the 360 ° divided by 24 hours a day which is the angle between the lines of radiation on the blue background is 15 °. Where these lines intersect the plane yellow, bind with the intersection point of the rod with the yellow plane quadrant.We then have the shadow of the rod is each of the lines that are pink on yellow background. Considering that in the north-south the sun casts the shadow of the rod at 12 am on the yellow background, right 15 ° we have the shadow of the 13 hours, the second rod 30 ° from north-south line have the 14 hours, the third rod at 15 hours, the fourth rod at 16 hours, and so on.
We observed a sundial and its construction. Gnomom a rod called shadow projected onto a plane or plane of the quadrant yellow, in this case horizontal. S called a blue plane is perpendicular to the rod and describes the sun's path in a complete circle, this means covering the 360 ° divided by 24 hours a day which is the angle between the lines of radiation on the blue background is 15 °. Where these lines intersect the plane yellow, bind with the intersection point of the rod with the yellow plane quadrant.We then have the shadow of the rod is each of the lines that are pink on yellow background. Considering that in the north-south the sun casts the shadow of the rod at 12 am on the yellow background, right 15 ° we have the shadow of the 13 hours, the second rod 30 ° from north-south line have the 14 hours, the third rod at 15 hours, the fourth rod at 16 hours, and so on.The ability to draw on the system enables us to figure dihedral easy understanding and construction, since there is only keep in mind that the blue print all lines which intersect each other forming rod 15 ° and the angle of the rod with the yellow background is exactly the latitude of the place where you put the sundial, as shown in geometry so that the sun projecting equally hours at equal angles, the rod must be parallel to the earth axis of rotation and this implies that the angle between the rod and the horizontal plane or the horizontal quadrant case, is equal to the angle between the plane of Ecuador and the point of land where the clock is located is nothing that latitude.
 As shown in the profile of the globe we are located in north latitude 40 ° angle defined from Ecuador.
As shown in the profile of the globe we are located in north latitude 40 ° angle defined from Ecuador.The clock is a horizontal plane that rests at the point P, our location. As shown in the drawing, 90 ° to form the Earth's axis and the latitude Ecuador least equals the angle yellow.
In our sundial, vertical and 90 ° quadrant are therefore the gnomon being a line parallel the earth's axis we have to the gnomon makes with the vertical at the same angle yellow vertical with the earth's axis, from which it follows that the latitude (90 ° minus the angle yellow) is equal to the angle of the gnomon and quadrant ( angle 90 ° less yellow). http://reloj-de-sol.blogspot.com/
http://cartografia-celeste.blogspot.com/
http://los-angulos-en-la-circunferencia.blogspot.com/

Figure observe different ways of representing the perspective of an object, a cylindrical projection axonometric orthogonal or parallel in which the figure are unchanged and linear perspective, central or tapered (similar to the values our view) in which the parallel always have a common point, called the leak.

Figure observe different ways of representing the perspective of an object, a cylindrical projection axonometric orthogonal or parallel in which the figure are unchanged and linear perspective, central or tapered (similar to the values our view) in which the parallel always have a common point, called the leak.
http://proyeccion-central-conica.blogspot.com/
http://proyeccion-gnomonica.blogspot.com/
http://la-perspectiva-conica.blogspot.com/
http://proyeccion-gnomonica.blogspot.com/
http://la-perspectiva-conica.blogspot.com/
http://perspectiva-conica-dinamica.blogspot.com.es/
If the vertical cut in another common point is we need the perspective of an inclined plane. http://perspectiva-de-cuadro-inclinado.blogspot.com/

The figure shows an icosahedron and a dodecahedron in plan and elevation. As we can see both are enrolled in a cube and its edges are centered ab in the center of each cube face. If we add the edge of the dodecahedron to the edge of the icosahedron b we see that are the size of the cube edge d. We also found that the edge of the cube is to the edge of the icosahedron as the edge of the icosahedron is the dodecahedron edge, so we need all three measures are in golden ratio d / b = b / a, a magical relationship between two segments whose ratio is 1.618 and appears continuously and needed in the order of nature. Also in the two projections in elevation of the figures the edge of the icosahedron is equal to the diagonal of each face of the pentagonal dodecahedron, since at any regular pentagon and its diagonal side are in golden ratio. http://la-proporcion- aurea.blogspot.com /
http://dodecaedro-en-icosaedro.blogspot.com.es/
 Figure formed by a wedge-shaped prism which has been introduced rhombic prism base another respect the hole produced in its displacement.
Figure formed by a wedge-shaped prism which has been introduced rhombic prism base another respect the hole produced in its displacement.
 Figure formed by a wedge-shaped prism which has been introduced rhombic prism base another respect the hole produced in its displacement.
Figure formed by a wedge-shaped prism which has been introduced rhombic prism base another respect the hole produced in its displacement. A regular octahedron is a regular polyhedron consisting of eight faces that are triangles equilateral. An equilateral triangle is a regular polygon, that is, the one with the sides and equal angles
A regular octahedron is a regular polyhedron consisting of eight faces that are triangles equilateral. An equilateral triangle is a regular polygon, that is, the one with the sides and equal angles( http://poligonos-regulares.blogspot.com/.)
The octahedron may be constructed by joining two pyramids joined by their basessquare.
The three diagonals of the polyhedron are the same size and hence both the plan projection as the projection to be square. The projection of a real face in magnitude as that corresponding to the auxiliary view B generates contour of the figure as a regular hexagon.

A regular tetrahedron is a regular polyhedron has four faces that are equilateral triangles. We have in section AA parallel to a face that always move the plane parallel to it is transformed into an equilateral triangle shrinking that grows into a point. One possible view of figure is a square floor B-is an auxiliary view perpendicular to the edges of the figure and the diagonals which are orthogonally intersect each other 90 ° and are of equal size.

This surface is generated by the evolution of a circle is transformed into an ellipse, so called surface evolution. It is also a ruled surface warped because we can link straight through his two foundations, the circle and the ellipse . If by extending the generators that connect the two curves have a straight, is a conical surface, hence we can say that is a truncated conoid.

A warped ruled surface can be obtained by straight lines connecting the two curves as Fig. The figure is formed by the junction of lines between two different guidelines sense of varying heights. As is that the lines forming the surface are always parallel to the plane of projection profile and is also a circumference with a connecting line through the middle of the figure, we have that the surface consists of two semi-conical. http://superficies-regladas-alabeadas.blogspot.com/
 A prism that has been subtracted an inner cylinder passing through the axis.
A prism that has been subtracted an inner cylinder passing through the axis.
A hyperboloid of one sheet with possible conic sections.
The hyperboloid of one sheet is generated by revolving a hyperbola about an axis. The smoothness of this curve makes cone used in aerodynamic design elements such as cars , boats, planes, etc..
 Figure symmetricallycomposed of two cones joined at their base in which a hole has been practiced with two inverted cones. Figure can engender by the revolution of a square which rotates around an axis so that its diagonal is perpendicular thereto.
Figure symmetricallycomposed of two cones joined at their base in which a hole has been practiced with two inverted cones. Figure can engender by the revolution of a square which rotates around an axis so that its diagonal is perpendicular thereto.
Intersection of a prism whose base is a rhombus, with a spherical surface and a cylindrical linked and in which has been practiced two hollow spherical.
 Helizoide rectum. Surface that generates a line orthogonal to a shaft rotates while moving through it, while remaining orthogonal.http://helicoides.blogspot.com/
Helizoide rectum. Surface that generates a line orthogonal to a shaft rotates while moving through it, while remaining orthogonal.http://helicoides.blogspot.com/ Sphere with a cylinder and a hemispherical hollow inside prism.
Sphere with a cylinder and a hemispherical hollow inside prism.
A prism in which the splice has been practiced to its vertices and edges, applying the same spheres and cylinders respectively. The standard allows for this type of surfaces do fine lines at the junction of the tangent surfaces to better define the shapes. The interior has undergone a hollow rectangle that is transformed in circumference, so it is a surface evolution that transforms the rectangle in another to which he is rounding the corners into a circle.

Figure consists of four parts with a hollow cylinder through it.

Figure consists of four parts.
It is constructed by the intersection of a sphere and a prism whose axis through its center and which has been subtracted another prism inside.

Prism which has been subtracted another prism and a cylinder.

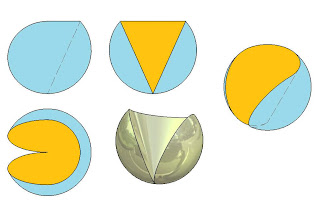
Sphere divided into eight equal parts to which has been removed four of its parts. The metal sphere reflects the environment, a perspective that can be calculated by calculating reflections.

http://proyeccion-estereografica.blogspot.com/
 Figure formed by the intersection of three orthogonal axes cylinders each other and which has been practiced in the form of a hollow prism.
Figure formed by the intersection of three orthogonal axes cylinders each other and which has been practiced in the form of a hollow prism.

trapezoid with two hollow cylindrical extrudate.

Figure formed by the intersection of three orthogonal axes cylinders together. Figure is projected in plan elevation and profile and contains an auxiliary view.

Iron in the form of a hyperbolic paraboloid.

hyperbolic paraboloid with three projections: a profile in plan and in elevation triangle and a trapezoid.

As shown in the figure the hyperbolic paraboloid can generate by a line while turning is displaced in a direction different from the plane that contains, instead of a line has taken a rectangle to give the character volume. On the ground we see the shape of a rectangle, the base moves at some point while turning, which generates the surface of the hyperbolic paraboloid with thickness.

A regular octahedron to which you have had a hollow cylinder.

A spring sired by a sphere moving along a helix is a coil. The helix is generated by a point moving in a circle while it travels through an axis perpendicular to its center. On the next page we see the transformation of a spherical cylindrical coil and other transformations: http://poliedroestrellado . blogspot.com /
 An icosidodecahedron is an Archimedean polyhedron that can be obtained by cutting the regular dodecahedron or regular icosahedron. Like all Archimedean polyhedron is formed by regular polygons but not all the same. The figure shows two sections of the polyhedron, one of them, in section CC determines the plane passing through the vertices of equilateral triangles five, so as to obtain a regular pentagon.
An icosidodecahedron is an Archimedean polyhedron that can be obtained by cutting the regular dodecahedron or regular icosahedron. Like all Archimedean polyhedron is formed by regular polygons but not all the same. The figure shows two sections of the polyhedron, one of them, in section CC determines the plane passing through the vertices of equilateral triangles five, so as to obtain a regular pentagon.

A regular icosahedron is a regular polyhedron , therefore has all equal sides, these being regular polygons. Its faces 20 equilateral triangles and is a dual polyhedron of the dodecahedron, this means that if we take the midpoints of each side and get the regular dodecahedron join, just as if we take the midpoints of the regular dodecahedron get the regular icosahedron.

This figure is an Archimedean polyhedron which begets the chamfering the corners and edges of the regular icosahedron. AA section shown inside the figure, the fact that the faces can be seen means that the object is a solid surface and not, or whether it is hollow.

regular dodecahedron faces colored for a better understanding of the piece. As you can see in color, from one projection to another match only a single face, this means that we have four faces on the ground, only one is seen in the elevation: the yellow. Of the four of the elevation is only one in the profile, the rose.

cone that has been removed and a cylindrical surface in the form of another bull. As penetration of the latter two figures is tangentially, warped curves that are produced have a figure eight, and are appropriate while the conical surface, as they are curves of intersection of two surfaces.

cone in plan and elevation with three possible sections conic of the same: when the cutting plane is parallel two generatrices, we have the hyperbola, when parallel to a generator and when we have the parable is not parallel to any we have the ellipse.

When the plane cuts the cone will turning produces various conic sections, in case the cutting plane is moved and comes to be tangent to a cone generatrix, the curved conical becomes a straight line which is called a degenerate conic. Another degenerate conic is when the cutting plane passes through the vertex producing two new possible figures, two straight lines which intersect the cone and passes through the vertex of the same or that the plane passing through the vertex uncut surface so that the degenerate conic is a point.

sphere with a hollow equilateral triangular prismatic base.

Figure of evolution that transforms a circle into a square progressively. A section at some point generates a curve between the square and circle, as we approach the square, the arcs of the new figure are centered increasingly remote.At the moment that is a square, the centers of the circumferences of the sides of the figure will be in the infinity .

Possible iron sections of a hyperbolic paraboloid-shaped, note that when the cutting plane BB contains a generatrix and is parallel to a master plan, the section is a straight line.

The elliptic paraboloid is a surface of revolution generated by revolving a parabola about its axis. The possible sections are parabolic, as shown in the figure a parabola, an ellipse or circle.

For the construction of the Archimedean polyhedra there are two types of truncation of the regular polyhedra, whose cutting plane that passes through the middle of the edge - type1-or truncation that passing approximately one third of the edge-type2-, so that the resulting polygon is regular, as in Fig.

The regular icosahedron can be constructed with pentagonal base pyramids whose sides are equilateral triangles, in Thus we have FF section is a pentagon. Likewise appears on the auxiliary view that follows the direction D, which is projected another regular pentagon. On the other hand in the projection obtained in the direction C, a face of the figure displayed in real form and contour of the polyhedron is a regular hexagon, while the section of it does not produce this figure, as the sides of the regular hexagon not are coplanar.

A cone-shaped solid that you have had two hollow spherical. As the hollow spheres are tangent to the cone divide this into three parts. The cutting plane AA which is tangent to the two spheres generates an elliptical section in which the points of tangency to the areas are the foci of the ellipse, according to the theorem Dandelin : http://curvas-conicas.blogspot.com /
 The cylinder shown in plan and elevation with axonometricisometric. While a circle in perspective is transformed into an ellipse, you can replace it, from its resemblance, by an oval in which to make their bows on the top center of the ring of the base. To make the minor arc from the center above a line perpendicular to one side of the diamond, where it cut straight to the horizontal axis we have the center of the other arc.
The cylinder shown in plan and elevation with axonometricisometric. While a circle in perspective is transformed into an ellipse, you can replace it, from its resemblance, by an oval in which to make their bows on the top center of the ring of the base. To make the minor arc from the center above a line perpendicular to one side of the diamond, where it cut straight to the horizontal axis we have the center of the other arc.

The cone in plan and elevation and axonometric isometric perspective representation. Similarly to the base has built an oval with the centers are marked in Fig. The ellipse has been replaced is a smooth curve to the oval and not noticed it among the different transition points as the link between two arcs of the oval. Another notable difference between the two figures is that if we draw the ellipse corresponding to the ring on which is inscribed in the oval, ellipse appears sharper, more eccentric, this means that the major axis dimension is more than the oval.

Cone in plan and elevation plane resting on a projecting vertical. To draw this figure should be raised from the cone first and then to project their views on the plant. On the ground the center of the circle is transformed into a minor axis of the ellipse and is given by the intersection of the horizontal line through which the vertex and the projection of the base of the cone of the elevation. While the major axis corresponds to the diameter of the cone of elevation, since this is true in magnitude.

To make the planes tangent to a cone from an external point P, join this point to the vertex V of the cone and have the He draws the line in the extension. Since the trace is made x1 g1 tangents to the base of the cone and points of tangency of the circumference are attached to the vertex of the cone. These straight lines joining the points of tangency with the tip of the cone are the planes tangent lines of the cone and the two planes tangent lines were determined by the x1-g1-a.

Surface of revolution formed by two cones and two spheres .The solid outer sphere contains a hollow cone which also contains a solid sphere tangent to it and in this second area other over the previous inverted cone. The two spheres are solid while the two cones are hollow. As the cone is based tangent to the sphere, the sphere divided in two figures.

 Figure formed by the intersection of three orthogonal axes cylinders each other and which has been practiced in the form of a hollow prism.
Figure formed by the intersection of three orthogonal axes cylinders each other and which has been practiced in the form of a hollow prism.
trapezoid with two hollow cylindrical extrudate.

Figure formed by the intersection of three orthogonal axes cylinders together. Figure is projected in plan elevation and profile and contains an auxiliary view.

Iron in the form of a hyperbolic paraboloid.

hyperbolic paraboloid with three projections: a profile in plan and in elevation triangle and a trapezoid.

As shown in the figure the hyperbolic paraboloid can generate by a line while turning is displaced in a direction different from the plane that contains, instead of a line has taken a rectangle to give the character volume. On the ground we see the shape of a rectangle, the base moves at some point while turning, which generates the surface of the hyperbolic paraboloid with thickness.

A regular octahedron to which you have had a hollow cylinder.

A spring sired by a sphere moving along a helix is a coil. The helix is generated by a point moving in a circle while it travels through an axis perpendicular to its center. On the next page we see the transformation of a spherical cylindrical coil and other transformations: http://poliedroestrellado . blogspot.com /
 An icosidodecahedron is an Archimedean polyhedron that can be obtained by cutting the regular dodecahedron or regular icosahedron. Like all Archimedean polyhedron is formed by regular polygons but not all the same. The figure shows two sections of the polyhedron, one of them, in section CC determines the plane passing through the vertices of equilateral triangles five, so as to obtain a regular pentagon.
An icosidodecahedron is an Archimedean polyhedron that can be obtained by cutting the regular dodecahedron or regular icosahedron. Like all Archimedean polyhedron is formed by regular polygons but not all the same. The figure shows two sections of the polyhedron, one of them, in section CC determines the plane passing through the vertices of equilateral triangles five, so as to obtain a regular pentagon.
A regular icosahedron is a regular polyhedron , therefore has all equal sides, these being regular polygons. Its faces 20 equilateral triangles and is a dual polyhedron of the dodecahedron, this means that if we take the midpoints of each side and get the regular dodecahedron join, just as if we take the midpoints of the regular dodecahedron get the regular icosahedron.

This figure is an Archimedean polyhedron which begets the chamfering the corners and edges of the regular icosahedron. AA section shown inside the figure, the fact that the faces can be seen means that the object is a solid surface and not, or whether it is hollow.

regular dodecahedron faces colored for a better understanding of the piece. As you can see in color, from one projection to another match only a single face, this means that we have four faces on the ground, only one is seen in the elevation: the yellow. Of the four of the elevation is only one in the profile, the rose.

cone that has been removed and a cylindrical surface in the form of another bull. As penetration of the latter two figures is tangentially, warped curves that are produced have a figure eight, and are appropriate while the conical surface, as they are curves of intersection of two surfaces.

cone in plan and elevation with three possible sections conic of the same: when the cutting plane is parallel two generatrices, we have the hyperbola, when parallel to a generator and when we have the parable is not parallel to any we have the ellipse.

When the plane cuts the cone will turning produces various conic sections, in case the cutting plane is moved and comes to be tangent to a cone generatrix, the curved conical becomes a straight line which is called a degenerate conic. Another degenerate conic is when the cutting plane passes through the vertex producing two new possible figures, two straight lines which intersect the cone and passes through the vertex of the same or that the plane passing through the vertex uncut surface so that the degenerate conic is a point.

sphere with a hollow equilateral triangular prismatic base.

Figure of evolution that transforms a circle into a square progressively. A section at some point generates a curve between the square and circle, as we approach the square, the arcs of the new figure are centered increasingly remote.At the moment that is a square, the centers of the circumferences of the sides of the figure will be in the infinity .

Possible iron sections of a hyperbolic paraboloid-shaped, note that when the cutting plane BB contains a generatrix and is parallel to a master plan, the section is a straight line.

The elliptic paraboloid is a surface of revolution generated by revolving a parabola about its axis. The possible sections are parabolic, as shown in the figure a parabola, an ellipse or circle.

For the construction of the Archimedean polyhedra there are two types of truncation of the regular polyhedra, whose cutting plane that passes through the middle of the edge - type1-or truncation that passing approximately one third of the edge-type2-, so that the resulting polygon is regular, as in Fig.

The regular icosahedron can be constructed with pentagonal base pyramids whose sides are equilateral triangles, in Thus we have FF section is a pentagon. Likewise appears on the auxiliary view that follows the direction D, which is projected another regular pentagon. On the other hand in the projection obtained in the direction C, a face of the figure displayed in real form and contour of the polyhedron is a regular hexagon, while the section of it does not produce this figure, as the sides of the regular hexagon not are coplanar.

A cone-shaped solid that you have had two hollow spherical. As the hollow spheres are tangent to the cone divide this into three parts. The cutting plane AA which is tangent to the two spheres generates an elliptical section in which the points of tangency to the areas are the foci of the ellipse, according to the theorem Dandelin : http://curvas-conicas.blogspot.com /
 The cylinder shown in plan and elevation with axonometricisometric. While a circle in perspective is transformed into an ellipse, you can replace it, from its resemblance, by an oval in which to make their bows on the top center of the ring of the base. To make the minor arc from the center above a line perpendicular to one side of the diamond, where it cut straight to the horizontal axis we have the center of the other arc.
The cylinder shown in plan and elevation with axonometricisometric. While a circle in perspective is transformed into an ellipse, you can replace it, from its resemblance, by an oval in which to make their bows on the top center of the ring of the base. To make the minor arc from the center above a line perpendicular to one side of the diamond, where it cut straight to the horizontal axis we have the center of the other arc.
The cone in plan and elevation and axonometric isometric perspective representation. Similarly to the base has built an oval with the centers are marked in Fig. The ellipse has been replaced is a smooth curve to the oval and not noticed it among the different transition points as the link between two arcs of the oval. Another notable difference between the two figures is that if we draw the ellipse corresponding to the ring on which is inscribed in the oval, ellipse appears sharper, more eccentric, this means that the major axis dimension is more than the oval.

Cone in plan and elevation plane resting on a projecting vertical. To draw this figure should be raised from the cone first and then to project their views on the plant. On the ground the center of the circle is transformed into a minor axis of the ellipse and is given by the intersection of the horizontal line through which the vertex and the projection of the base of the cone of the elevation. While the major axis corresponds to the diameter of the cone of elevation, since this is true in magnitude.

To make the planes tangent to a cone from an external point P, join this point to the vertex V of the cone and have the He draws the line in the extension. Since the trace is made x1 g1 tangents to the base of the cone and points of tangency of the circumference are attached to the vertex of the cone. These straight lines joining the points of tangency with the tip of the cone are the planes tangent lines of the cone and the two planes tangent lines were determined by the x1-g1-a.

Surface of revolution formed by two cones and two spheres .The solid outer sphere contains a hollow cone which also contains a solid sphere tangent to it and in this second area other over the previous inverted cone. The two spheres are solid while the two cones are hollow. As the cone is based tangent to the sphere, the sphere divided in two figures.

The figure is formed by an area that has been subtracted an elliptical cylinder.
 A cube is crossed by two cones whose bases are circles tangent to two adjacent faces of the same. The intersection of the two cones produces two ellipses, an ellipse which is the greatest X corresponding to the zone of interference of the two cones and a lower ellipse which is formed by two parts, one corresponding to a cone penetration in the other and conversely.
A cube is crossed by two cones whose bases are circles tangent to two adjacent faces of the same. The intersection of the two cones produces two ellipses, an ellipse which is the greatest X corresponding to the zone of interference of the two cones and a lower ellipse which is formed by two parts, one corresponding to a cone penetration in the other and conversely.In the elevation can be seen as the intersection corresponding to the larger ellipse is given by the bisector m ab sides of the cube. VH ends of the axis of the ellipse correspond to lower G zone between these points, which are the intersection of the generatrices of the cone contour (s-LK to point V, for example).
 The figure is formed by a cube that has been subtracted from a cylinder in one direction and a prism on the other, both surfaces radiated tangent at a generatrix.
The figure is formed by a cube that has been subtracted from a cylinder in one direction and a prism on the other, both surfaces radiated tangent at a generatrix.The figure is formed by two cubes composition so it is a polyhedron compound: http://poliedroscompuestos.blogspot.com/
Polyhedra page cuts compounds.
 A cube that are rounded vertices and edges is pierced through the center of each of its sides by three cylinders of the same diameter.
A cube that are rounded vertices and edges is pierced through the center of each of its sides by three cylinders of the same diameter.

An object of revolution with its lid shown in partial cutaway elevational imaginary so that its cut surface is shown with a 45 ° striped represented by parallel and equidistant lines. As the object and the cover are separate elements must also be scratching different but always at 45 °, to differentiate can vary the direction of striped or vary the distance between the parallel lines of scratching. Thanks to semicorte is provided that can be seen in elevation within the part in the middle of it and the outside in the other half.

In a hemisphere has been practiced a hollow torus-shaped tangent to its surface, so that the line of contact of both surfaces appears in the plant and is coincident with the elevational contour of the hemisphere, the hemisphere divided into two parts.

A sphere has been pierced by another inner sphere which has moved in a diametrical direction line of the field, generating a surface shaped hollow capsule. perspective representation appears in the middle of the figure showing the interior thereof.

This figure is formed by the intersection of a cone and a bull. The cone has been subtracted from the bull creating the gap can be seen in Fig. The intersection is calculated in the usual manner are passed planes, for example horizontal, that cut both figures. The intersection of each plane with the two figures we determined two curves defined at their intersection points of intersection of the two surfaces. The horizontal planes intersect the cone according to circumferences, while cutting the bull with much more complex curves, so that resolution of the exercise is somewhat complicated. If we take planes orthogonal to the axis of revolution of the cut cone, being a surface of revolution, as parallel circles of different diameters and also cut cone parabolic curves, since the axis of revolution of the torus is perpendicular to the generatrix of the contour the elevation of the cone.

Sphere which has removed a triangular based prism.

 A cube that are rounded vertices and edges is pierced through the center of each of its sides by three cylinders of the same diameter.
A cube that are rounded vertices and edges is pierced through the center of each of its sides by three cylinders of the same diameter.
An object of revolution with its lid shown in partial cutaway elevational imaginary so that its cut surface is shown with a 45 ° striped represented by parallel and equidistant lines. As the object and the cover are separate elements must also be scratching different but always at 45 °, to differentiate can vary the direction of striped or vary the distance between the parallel lines of scratching. Thanks to semicorte is provided that can be seen in elevation within the part in the middle of it and the outside in the other half.

In a hemisphere has been practiced a hollow torus-shaped tangent to its surface, so that the line of contact of both surfaces appears in the plant and is coincident with the elevational contour of the hemisphere, the hemisphere divided into two parts.

A sphere has been pierced by another inner sphere which has moved in a diametrical direction line of the field, generating a surface shaped hollow capsule. perspective representation appears in the middle of the figure showing the interior thereof.

This figure is formed by the intersection of a cone and a bull. The cone has been subtracted from the bull creating the gap can be seen in Fig. The intersection is calculated in the usual manner are passed planes, for example horizontal, that cut both figures. The intersection of each plane with the two figures we determined two curves defined at their intersection points of intersection of the two surfaces. The horizontal planes intersect the cone according to circumferences, while cutting the bull with much more complex curves, so that resolution of the exercise is somewhat complicated. If we take planes orthogonal to the axis of revolution of the cut cone, being a surface of revolution, as parallel circles of different diameters and also cut cone parabolic curves, since the axis of revolution of the torus is perpendicular to the generatrix of the contour the elevation of the cone.

Sphere which has removed a triangular based prism.

Prism which has been subtracted from another perspective.
 A cube that has been subtracted from each of their faces another prism whose edges are tangent to their faces. The intersection of the prisms in the three directions generates this curious figure.
A cube that has been subtracted from each of their faces another prism whose edges are tangent to their faces. The intersection of the prisms in the three directions generates this curious figure. In the figure we can see a cube that has been subtracted from a cylinder placed at an angle relative thereto.
In the figure we can see a cube that has been subtracted from a cylinder placed at an angle relative thereto. In a cube have been practiced two hollow cylindrical one which is on the inside of the figure and one whose axis coincides with an edge of the cube.
In a cube have been practiced two hollow cylindrical one which is on the inside of the figure and one whose axis coincides with an edge of the cube.In view can be seen the intersection of the two cylinders.
 A cube is traversed by a cylinder and a prism, two tangents thereto. The intersection between the two causes hollow figures in profile tangent arcs which are the projections of the ellipses of intersection of two surfaces hollow.
A cube is traversed by a cylinder and a prism, two tangents thereto. The intersection between the two causes hollow figures in profile tangent arcs which are the projections of the ellipses of intersection of two surfaces hollow.
Area in which it has been practiced a hollow interior formed by two cone and a cylinder. In the perspective projection, the vertices of the cones coincide with points of their bases, there appears only represented a cylindrical shape.

the figure is formed by a cube that has been subtracted two tangents at their circumferences bulls to the faces thereof. The bulls are centered on the midpoint of the opposite edges of the cube. As the circumferences of the bulls are tangent to the faces of the cube, are also displaced to the adjacent faces so cubed divided into three parts.

figure formed by an area that has been stripped from the top other field, generating an orange surface and the bottom cylinder and a prism, causing the surface blue.

Industrial piece formed by links cylindrical surfaces and prisms in the interior of the figure have been performed several holes of different diameter cylindrical.

the figure is formed by the union of two pyramids. Its contour in plan, elevation and profile, a triangle, another, and a square, respectively.

inside a sphere is drawn a regular pentagon and are rotated about a diameter thereof. The inner surface is generated causing the empty space has hollow torus shaped regular pentagonal section.

the figure is formed by an ellipsoid-shape formed by rotation of a semi-ellipse about its major axis in this case, the you have been away a regular pentagonal prism
 figure formed by the intersection of prisms and cylinders.
figure formed by the intersection of prisms and cylinders.
in the figure we see AA cut by parallel planes in which it changed its direction to intercept the opening of the piece. As in the ends of the cutting plane are marked lines of greater thickness, in the change of direction of the plane cutting the workpiece is also the same.

a cylinder to which it has been practiced other four hollow cylindrical and prismatic in its upper .

figure formed by a prism which is twisted and have rounded ends.

in the figure has been practiced a cylindrical hole and a prismatic, in this latter has been practiced a hole being shown in elevation in detail by a partial cut.

Industrial piece displayed in the dihedral system with an auxiliary view and two orthogonal projections in perspective.

cylinder which is subtracted a prism and three cylindrical holes, apart from their views dihedral is shown a cut of it and its representation in perspective.

in Figure have a surface of revolution generated by a trapezoid that has revolved around an axis to which it has a rounded bottom edge. In the upper surface have been performed using an array polar, concentric cylinders tangent to the contour the circumferences of the annulus.

figure formed by a prism and interference from multiple cylinders.

We observe a hexagonal prism with a hollow spherical bearing in which three central axis in a hexagonal prism whose bases are available polar vertices tangents to the circles hollow prism faces generated by the inner sphere. We can see in the section of the vertical plane through the points BB the visible part of the spherical surface in green and purple prisms and blue. The court can always see what is behind the cutting plane.

Figure composed of extruded shapes intersecting arcs as equidistant.
 The figure shows a hollow sphere with three interior hollow cylinders with three different bases. We can observe in detail on a larger scale, this scale is that corresponding to the piece in reality, not drawing on the ground and in elevation, this means that the detail is six times larger in the drawing in reality. In the elevational view of the figure shows a cut of the same coinciding with the axis of horizontal symmetry of the piece. As this corresponds to a cut plane through the center coincides with an axis of symmetry, no details are given normalized cut or letters which pass through the vertical plane of cut.
The figure shows a hollow sphere with three interior hollow cylinders with three different bases. We can observe in detail on a larger scale, this scale is that corresponding to the piece in reality, not drawing on the ground and in elevation, this means that the detail is six times larger in the drawing in reality. In the elevational view of the figure shows a cut of the same coinciding with the axis of horizontal symmetry of the piece. As this corresponds to a cut plane through the center coincides with an axis of symmetry, no details are given normalized cut or letters which pass through the vertical plane of cut.
Figure observe a cone to which is have subtracted two cones, a hollow cone whose axis is perpendicular to the larger and a cone cone whose axis is parallel thereto. The intersection of the larger cone with the other two curves generates two warped, ie curves which can not affect all points on a plane.

Figure observed the importance of the cuts when represent the parts. The vertical plane passing through the points defined with precision BB cutting the detail which can be seen the circumferences concentric cylindrical surfaces of FIG. While the horizontal plane determined by the points AA, defined with precision the angle between the direction of the axes of the cylinders relative to the structure of the piece.

In the figure we can observe a cylindrical hollow sphere with two holes and two prismatic . At the same time it has taken a quarter of the field, revealing more clearly the hollow interior of the four internal communications.
 In the figure we can observe a hexahedron (figure formed by six sides, in this case two pyramids joined at the base) with two spherical recesses, one of which intersects two sides and the other field. The other hollow sphere intersects the sphere as a circle before cutting. The area also intercepted four sides of the figure, cutting them in four circles.
In the figure we can observe a hexahedron (figure formed by six sides, in this case two pyramids joined at the base) with two spherical recesses, one of which intersects two sides and the other field. The other hollow sphere intersects the sphere as a circle before cutting. The area also intercepted four sides of the figure, cutting them in four circles.It is a difficult piece of sense, especially in its projection in the profile, in which one of the circles generated by the inner sphere on one side matches with one side that turns into a straight line on this projection, which is why you can not see the circle as it coincides with the face in one line.
The auxiliary view A to view the matching circles that show the background in white.

In the figure we can observe the composition of a figure generated with prisms cylinders and cones.

prism with two cylindrical holes and their respective intersections.

cylinder in which two holes have been performed, one cylindrical and one prismatic hexagonal base.

prism with two holes, one cylindrical and one conical blue yellow, with their respective intersection.

hyperboloid regulated with a hollow hexagonal prism, with its rounded top.

figure formed by binding of prisms and cylinders.

prism to which he has made a twisting of the upper side generating curved surfaces on the sides in the shape of hyperbolic paraboloids.

in the figure we can observe a polyhedron which has been subtracted from a sphere. As the center of the sphere does not pass through the center of the polyhedron but is displaced, have to cut the faces by a larger circumference side.

cylinder portion to which it has been subtracted two prisms.
 prism formed by the union of two (blue and green vertical faces), and which has been cut by two planes slanted faces generating yellow and orange.
prism formed by the union of two (blue and green vertical faces), and which has been cut by two planes slanted faces generating yellow and orange.
cylinder in which two holes have been performed and a prismatic cylindrical .

piece in perspective representation which is made by removing a fourth imaginary cutting thereof.

piece formed by the intersection of four cylinders and a hollow prism.

solid prism to which it has been spliced vertices and edges and which has practiced half a hollow cylindrical capsule and another.

prism formed by the difference of two holes and their respective intersection, a pink cylindrical and conical another yellow.

ellipsoid with a hollow spherical centered within.

cube in which two holes have been practiced with hexagonal prism shape.

prism in which a hole has been practiced regular hexagonal cross section.

prism with a cylindrical hole and another loop of rectangular section.

a sphere to which it has been subtracted two square-based pyramids , one inverted over the other.

an area that has been stripped of another sphere, a prism and a cylinder.

area that has been stripped of one eighth of it and several cylinders and prisms.

area in which has practiced a form of hollow pentagonal prism base. The intersection of the prism faces with the sphere are circles.

area in which a hole has been practiced in the form of elliptical cylinder.

area in which holes have been practiced to form cylindrical, spherical and toric.

intersection of a prism base and a triangular area in which two holes have been performed, one spherical and one prismatic.

piece consists of a sphere that has been removed and the fourth that has been practiced a hollow cylindrical, conical and other loop.

area that has been stripped several pieces of the same, as well as various cylinders and prisms.

area that has to be subtracted from an inner hub so that the area of the cross vertices of the cube, showing the eight holes corresponding to it.

area that have been removed cylinder and a prism.

way to show the dihedral system section in elevation of a detail, and details for two parts of the piece A C. The parties who want to highlight are marked with a circle, are named and drawn on a larger scale in another part of the paper with a letter indicating parentheses and the scale of the drawing referred to.

Views dihedral of a piece with their representation in axonometric and the cut through the plane AA. In the analysis depicted only what you see behind the plane of the section after turning 90 ° and projecting in the direction orthogonal to the plane.

figure whose three projections in plan, elevation and profile H.

shaped pentagonal prism which have practiced two cylindrical holes.

In the piece has made a turn cutting planes passing through the AA.As these planes are broken and the cutting direction is defined by the vertical (as we see from the orthogonal projection to east), from the point where it breaks the line through which the cutting plane-that is, from this point to the end of the piece, that is, the entire area that appears horizontally striped rotated until it coincides with the vertical plane.

here we observe a cone in plan, elevation and profile. It embodied have practiced three holes in three new cones.

in a prism there have been two cylindrical holes in one direction and another in another. The result of both plant interference is a figure with a roughly between circle and square.

in a hub has been practiced two hollow cylindrical tangent at their bases.

this figure is the result of interference between a pentagonal prism and a triangular prism.

in a prism has been practiced on its four vertical edges hollow cone-shaped and their axis a cylindrical hole.

a figure similar to above but without the internal cylindrical hollow.

a figure formed by the intersection of two cylinders leaving a gap inside the cylinder-shaped prism and a link between the pieces that remain.

a prism has been practiced a conical recess seen in its two vertical intersection hyperbolic curves horizontally and a circumference.

to have a cone practiced hollow conical and cylindrical.

In a regular octahedron (dipyramid), which is a polyhedron formed by two pyramids joined by their bases and equilateral triangular faces, has been subtracted from an inner sphere whose center coincides with that of Fig. As all the faces have the same arrangement relative to the center have all sections or hollow sphere produced are equal. We note that the auxiliary projection in the three axes or distance between vertices are equal, corresponding to the vertices that are observed in the plant and corresponding to the vertices comprising the vertical line.

here is another regular octahedron with different projections to that has taken away a cylinder.

in a bucket have practiced two holes, a cylindrical section and a regular pentagonal prism. Elevation in a meridian section projecting elliptic curves of the interference of the two surfaces.

in a bucket two holes have been practiced in the form of triangular based prism on two of its faces.

piece composed of a prism and cylindrical hollow cylinder and another prism.

on a sphere is tangent cone base by one of its diameters dividing it into two parts, the one in green and yellow. The conical hole pierces the hemisphere yellow exposing the interior of the red.

a hexagonal prism base is hollowed by a cylinder located inside obliquely. In the drawing have different projections and auxiliary views of Fig.

the figure is formed by the intersection of a cylinder and a prism of triangular base. On the axis of the figure has practiced other cone-shaped hole.

Figure is an area which has downplayed three parts: an internal prism, an inner cylinder that is tangent to the faces of the prism and a prism through the area by removing a quarter of it.

In the piece we see the remark following the UNE. The basic principles of the dimension we need to be the symmetric part are first determined the symmetry axes that are defined by alternating short and long segments. Once you have placed the axes mark the distance between them. Then put the dimension of the circles and arcs of the figure. If not checked the center is the diameter symbol, if the arc is greater than 180 ° is bounded as diameter or less if done as radio. To narrow the radius gets the letter R if the dimension line does not pass through the center.

Figure observe a prism to which he underwent two cylindrical holes, one bound with a piece of tangent sphere. The intersection of both cylinders is determined by common generatrices and the warped curve intersection of sphere and cylinder that connects both. The warped curve is determined by the curve of intersection of the plane that intersects the sphere and intersecting the cylinder. Each plane determines a point on the curve warped.

Figure observe a torus without holes, ie, the figure generated by revolving a circle around a secant not incident on its center. Inside the torus has been practiced a prismatic hollow half of the figure, from the middle of the figure is taken half of the rhombus which is the base of the prism is rotated around an axis of the rhombus generating a surface of revolution hollow inside of the figure and which passes through the prism base downwards.

Cube which is subtracted from an internally hollow prism.

cylinder which has been practiced a cylindrical hollow inside. As we can see the cylinders are tangent to its generatrices, it causes a gap in the profile as a bow tie.

A cube is crossed by two hollow cylinders and solid prism oblique solid in it.

Here we see a yellow key with their three dihedral projections, plan, elevation and profile. At the right is an oblique view of the key plan corresponding correlated with their projections. A projection of the latter could either be an axonometric representation, since this is a cylindrical projection on the plane orthogonal, as is the system dihedral . So one of the important issues is that we use dihedral for the projections of the part views are representative of their size and show their faces in true form to the greatest extent possible.

In the figure we can see the sights dihedral in one piece. To the right of it have three axonometric projections thereof. At the industrial parts of objects and are interested in using a perspective to better display the piece. This perspective should be an axonometric as a perspective in which the parallels are maintained, this means that if the part has parallel edges in the drawing axonometric persist.

in the figure we can observe an area that has been practiced two holes, one formed by a vertical cylinder and a composition consisting of two cones with the same base.

in the figure we can observe an area that have been subtracted three orthogonal cylinders.

figure formed by prisms linked to arcs generated at the extrusion surfaces of revolution of rectangular section.

Figure observe binding of six cones with a hexagonal prism base. The surfaces of the cones are tangential to the vertical faces of the prism at the top while the bottom intersect the base of the prism as hyperbolas. inner cones tangent at its generatrices are represented in blue on top and green at the bottom while the outer appear yellow in the top and the bottom orange.

prism with holes generated by the intersection of three cylinders.

in an area have been practiced six spherical recesses intersect with each other.

in the field have been performed the six holes of the previous figure, have been practiced other six holes symmetrical with respect to a meridian plane of the sphere and the interior thereof has been practiced other hollow spherical simultaneously intercepts the 12 areas.

Figure observe a cylinder which is traversed by another cylinder, generating as the intersection of the two surfaces two ellipses and four identical parts. The auxiliary view projected in the direction A of the ellipse becomes a straight and the other remains unchanged, because the ellipse coincides with the plane of projection.

Figure consists of a cube that has been practiced a hollow cube. Within the gap contains half sphere centered.

The figure is formed by the union of a prism and a cylinder in which a hollow prismatic been practiced.

figure formed by a cylinder crossed by two orthogonal horizontal cylinders , by a prism whose axis passes through the figure and a cone at the base of the cylinder in which a hole is practiced with a pyramid.

in a figure formed by a prism and a hollow cylinder practiced generated three different cones.

a figure contains two bulls start out hollow interior for the outside and then become solid.

a prism is crossed by several irregular cylinders causing this.

here is another prism also crossed by several cylinders in orthogonal directions.

a sample piece their dihedral view and a sectional elevation with a fourth imaginary.

in the figure shows an object formed by the intersection of a cone and a prism. The intersection of the faces of the prism with the conical surface causes two hyperbolas, curves that determine them together a surface called hyperbolic cylinder. The cone has been subtracted from the above solid hyperbolic cylinder causing the figure shown in the representation.

in the figure shows a cone that has been subtracted from a cylinder in which rests a hemispherical end. As the cylinder is tangent to a generating base is coincident with it, so it appears continuously. The sphere is tangent to the cone so that the circumference of intersection or contact between the cone separates them into two parts, the blue and yellow.

in the prism have been performed three hollow cylindrical two concentric passing through the vertex and the other passes through the midpoints of two opposite edges.

prism to which have so far limited number of cylinders.

a sphere contains inside two hollow pyramids joined at their bases.In each of the sides or faces of the pyramids have risen to the outer hollow prism. The figure is a sphere therefore with six hollow triangular section prism directed toward the center thereof.

in an area have performed three holes, a prism and two concentric cylindrical.

a cone which has been subtracted from a pyramid regular hexagonal basis.

the figure is generated by the intersection of two triangular prisms orthogonal basis, one in the direction of plant and another in the direction of the elevation, hence its two projections in plan and elevation are equilateral triangles. Then it has been practiced a cylindrical hollow in the vertical direction, which causes to display on an elliptic curve profile.

Figure observe a piece composed of a hollow cylinder threaded inside and a sphere attached to the cylinder. The representation shows a cutaway elevation imagery of the piece as if it had taken a room.

the figure is composed of three parts: a sphere of yellow color in the center with an inner cylindrical hole whose axis passes through the center of the and whose bases are supported cylinder two spherical caps red and blue respectively.

the figure comprises two intersecting cylinders and other solids internal intersection of two hollow cylinders.

The piece is formed by a cylinder that has been subtracted inside four pieces of areas together account for 180 °. The intersection with the pieces of spheres produced in the bases of the cylinder circular sectors whose angle is 45 ° and rectangles on the cylindrical surface suitable to it. Flat inner walls appear blue while the spherical orange.

Figure is formed by a torus (donut-shaped figure) which has been subtracted from a cylinder surface and tangent to the circumference of its base profile .

the figure is formed by the intersection of a cylinder with six bulls that are arranged in a polar matrix. The intersection of the cylinder and causes the bulls "circles" warped deformed while blue surfaces are colored yellow bulls.

the figure shows an area that has been subtracted inside a prism. The prism intersects the sphere according to plans that are circles. In the plan projection observed that the base of the prism is a square. If all the projections were square circumferences would be joined together by a single point, which would decompose in Fig spherical caps as many sides has the cube. As noted in the auxiliary view, the height of the base causes other than a perfect square, which connects the spherical surface caps in a region greater than a point, and is therefore a single piece and not several.

an ellipse in the revolution of its minor axis causes an ellipsoid. In practice it several holes, one cylindrical and the other corresponding conical and cylindrical inside yellow.

Theorem Monge
If you do 3 circumferences common tangents 2-2, 3 points of intersection of each pair of tangents are aligned. The theorem is true for external and internal tengentes, indiscriminately and combined.

One application we have in the next exercise generalized the above theorem in space. Given 3 balls to determine the trace of the plane resting on them. We the 3 tangent cones both-like cones containing ice-balls, and the three apexes of the cones is the trace of the plane. We forecast a possible elevation to LT perpendicular to the horizontal trace to facilitate the exercise and we had a vertical trace tangent to the rebels of the spheres. At the points of tangency supports the plan, detail that can be lowered to the ground.
http://teoremas-de-geometria.blogspot.com/2012/03/teorema-de-monge.html

Development of a surface.
The development of a surface is obtained on the plane figure spread on a plane. Is as if it were a figure surrounded by a fine material on its surface to be opened along the edges. As you open each of their faces the doblaríamos to place them in a plane of the drawing, being extended envelope of the figure on the plane. In developing the figure on a plane to obtain the true size and shape of faces. To construct the development of a pyramid, make a turn of the faces taking as axis of rotation of the plane edge t2 corresponding to the base. To make the turn project the apex of the pyramid or the horizontal plane and from this point O 'do a line perpendicular to the trace m2 t2 plane corresponding to the face. Making center at the point of intersection of this Z2 perpendicular to the trace of the plane, we turn taking as radius the distance from the center Z2 until the apex of the pyramid O. The arc corresponding to the vertex determines turn at the intersection with the perpendicular m2 at the apex depressed t2 (O2), which together with the ends of the trace of the face is your face downcast t2 of the pyramid (in the drawing appears in red). The three faces blasted together with the base of Fig determine Figure stretched over the plane, in geometry called the development thereof. We can turn the red triangles on the sides that touch the base of the figure (t1 t2 t3) and thus the pyramid is built in three dimensions.
In the drawing we see the exercise resolved in the dihedral system. To make the gloom of the faces, we take one of them, such that face whose plane cuts the horizontal as the line t2. Making from the apex of the pyramid a perpendicular to this line m2 and taking the point of intersection of both Z2, we center it with the distance from that point Z2 until the apex of the pyramid folded O2 '. To make the lowering of the triangle on a vertical plane take the height of the vertex of the pyramid h that is in the true magnitude and elevation from the vertex placed on the ground orthogonally to the line O m2. In this way we obtain the vertex of the pyramid depressed O2 'and the slope of the face, defined by the points Z2-O'2. then doing as we said center at the intersection of the perpendicular to the trace of the face, Z2, we make the arc with the radius Z2-O'2 and where this arc cutting the perpendicular extension of m2 have the folded top of the pyramid (O2) and therefore the abatement of this face, as the others: the be in the axis of rotation, remain unchanged.This point is joined to the ends of t2 and we have every downcast face. To eliminate the other two sides proceed the same way. Blasted three triangular faces (red) with the base of the figure (in yellow) define an oblique development of the pyramid, which could cut the outline and bend at the intersection of each triangle with the yellow red , thereby obtaining the figure constructed, for example on paper. developments types: may be developed bylines passing through a center , also called radiated. A figure by parallel lines can be developed as with the radiating surface of vertex improper : prisms and cylinders. This development corresponds to improper point radiated surfaces such as cones and pyramids. By triangulation , this is obtained by dividing the surface sides of the triangular shapes. Developments approximate are those used for the warped surfaces of double curvature and , surfaces that can not be developed but forms obtainable approximate its extension in the plane.
Pages of figures dihedral system: http://piezas-vistas-y-cortes-1.blogspot.com/
http://piezas-vistas-y-cortes-2.blogspot.com/
http://piezas-vistas-y-cortes-3.blogspot.com/
http://piezas-vistas-y-cortes-4.blogspot.com/
http://piezas-vistas-y-cortes-5.blogspot.com/
http://piezas-vistas-y-cortes-6.blogspot.com/
http://piezas-vistas-y-cortes-7.blogspot.com/
http://piezas-vistas-y-cortes-8.blogspot.com/
http://piezas-vistas-y-cortes-9.blogspot.com/
http://piezas-vistas-y-cortes-10.blogspot.com/
http://piezas-vistas-y-cortes-11.blogspot.com/
http://piezas-vistas-y-cortes-12.blogspot.com/
http://piezas-vistas-y-cortes-13.blogspot.com/
http://piezas-vistas-y-cortes-14.blogspot.com/
http://piezas-vistas-y-cortes-15-poliedros.blogspot.com/
http://piezas-vistas-y-cortes-16.blogspot.com/
http://piezas-vistas-y-cortes-17.blogspot.com/
http://piezas-vistas-y-cortes-18.blogspot.com/
http://piezas-vistas-y-cortes-19.blogspot.com/
http://piezas-vistas-y-cortes-20.blogspot.com/
http://piezas-vistas-y-cortes-21.blogspot.com/
http://dibujo-de-piezas.blogspot.com/







No hay comentarios:
Publicar un comentario